Tous les Articles
Les articles sur les Récréations mathématiques (Carrés Magiques…) sont regroupés en trois sections :
Definitions et Propriétes
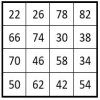
Progressions arithmétiques et carrés magiques
Certaines progressions arithmétiques génèrent des carrés magiques par addition, intéressants par leur composition, que nous nous proposons de présenter, de préciser et de développer. Sommaire1 Le carré magique normal.2 Des nombres impairement pairs.3 Une suite de sous-carrés de quatre cases.4 Suite normale issue du carré naturel d’ordre n = 3.5 Remarques à propos des progressions… Lire la suite »Progressions arithmétiques et carrés magiques
Nicolas de Cues et la quadrature du cercle
Nicolas de Cues (1401 – 1464), de son vrai patronyme Nikolaus Krebs, connu aussi sous le nom de Nicolas de Cuse, est un théologien, philosophe, humaniste, mathématicien et prélat allemand, né à Cues, dans le territoire du Westrich (Palatinat).Docteur en Droit, il est nommé cardinal en 1448, puis évêque de Brixen en 1450. Nicolas de… Lire la suite »Nicolas de Cues et la quadrature du cercle

Un curieux carré magique d’ordre n = 12
Ce carré magique normal d’ordre n = 12, de Constante magique M12 = 870, a été trouvé dans les papiers de Benjamin Franklin ( 1706 – 1790 ) après sa disparition, sans aucune mention d’origine. Le correspondant de Benjamin Franklin n’a pas laissé son nom. Ce curieux carré magique anonyme a été présenté par Paul C.… Lire la suite »Un curieux carré magique d’ordre n = 12

Les permutations figurées dans les tables d’addition et de multiplication
Cet article vient en complément du livre récemment paru : René Descombes – A la recherche des permutations figurées – (Amazon) Sommaire1 Les permutations figurées dans la table d’addition.2 Les permutations figurées dans la table de multiplication. Les permutations figurées dans la table d’addition. Considérons tout d’abord, la table d’addition classique, dite de Pythagore ; c’est… Lire la suite »Les permutations figurées dans les tables d’addition et de multiplication
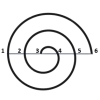
La Sextine d’Arnaut Daniel
Sommaire1 Arnaut Daniel2 La Méthode de la Spirale3 La Quenine de Raymond Queneau4 Les nombres de Queneau5 Les nombres de Sophie Germain6 Une Méthode de construction des carrés latins : La Méthode de la Spirale. Arnaut Daniel La Sextine est une structure poétique particulière inventée par le troubadour provençal du Moyen Age Arnaut Daniel ( 1150… Lire la suite »La Sextine d’Arnaut Daniel

Lexique des termes utilisés dans l’étude des carrés magiques
Bien que les expressions mathématiques soient définies et expliquées dans les différents articles, il peut être utile de de les définir toutes en un lieu unique.
Études et Jeux (2005-2015)
Sur cette page sont proposés des études, jeux, programmes… concernant les carrés magiques, écrits et réalisés par les lecteurs de ce blog. Si vous souhaitez également partager une de vos réalisations, contactez-nous !
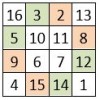
Les Carrés Magiques Associés
Sommaire1 Quelques définitions1.1 Les nombres complémentaires1.2 Les cases complémentaires1.3 Les carrés magiques normaux de type associé2 Propriétés générales des carrés magiques de type associé3 Les carrés magiques de type associé n =44 Les carrés magiques de type associé n =5 Quelques définitions Les nombres complémentaires Dans la suite naturelle des nombres entiers de 1 à… Lire la suite »Les Carrés Magiques Associés

Choix à priori de la constante linéaire des Carrés Magiques : Propriétés générales
Rappel de quelques propriétés générales des carrés magiques. Sommaire1 Propriété des quatre opérations2 Propriété des permutations figurées diagonales 3 Propriété des permutations figurées diagonales maximum4 Conventions et symboles Propriété des quatre opérations On n’altère pas la magie d’un carré magique lorsque l’on augmente ou diminue tous ses termes d’un même nombre w, ni lorsque l’on multiplie… Lire la suite »Choix à priori de la constante linéaire des Carrés Magiques : Propriétés générales
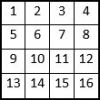
La magie du carré naturel
Le carré naturel d’ordre n = 3 se présente sous les huit formes classiques ci-dessous. On propose d’assembler au carré, quatre de ces grilles, de façon à obtenir une grille « magique » d’ordre n = 6 de 36 cases. On demande de dénombrer ces assemblages magiques, et d’en dresser le catalogue. On dénombre : combinaisons de ces 8… Lire la suite »La magie du carré naturel

Les Carrés magiques de Thomas Mann
Dans le roman de Thomas Mann, « Le Docteur Faustus – La vie du compositeur allemand Adrian Leverkühn racontée par un ami » ( 1947 ), le narrateur, Serenus Zeitblom, s’exprime ainsi qu’il suit à propos de la chambre qu’occupe Adrian Leverkühn dans le ville de Halle . Au-dessus, sur le mur, des punaises fixaient une gravure, un… Lire la suite »Les Carrés magiques de Thomas Mann

Le carré magique de Gaudi
Sur l’une des façades de la « Sagrada Familia », la cathédrale de Barcelone, se trouve sculpté dans la pierre, un carré numérique, dont la constante « magique » est M’4 = 33, soit l’âge présumé de Jésus Christ lorsqu’il a été crucifié. Notons également que la somme des quatre cases centrales est également égale à 33. C’est Antoni… Lire la suite »Le carré magique de Gaudi

Le Crible d’Eratosthène revisité
Ératosthène de Cyrène est un astronome, géographe, philosophe et mathématicien grec du IIIe siècle av. J.-C.. Érudit reconnu par ses pairs, considéré comme le plus grand savant de son époque, il travailla dans les domaines des mathématiques, de l’astronomie, de la poésie, de l’histoire , de la musique….Dans le domaine de la géographie, il a… Lire la suite »Le Crible d’Eratosthène revisité
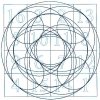
Propriétés du Carré Magique de Dürer
Les cercles magiques du carré de Dürer On peut inscrire dans un cercle vingt huit configurations différentes des 4 termes (dont les 4 permutations figurées : 11*, 12*, 51*, 52*) donnant la constante magique dans le carré magique de Dürer. Ces formations sont matérialisées dans les grilles ci-après, extraites de la grande planche des 86 combinaisons… Lire la suite »Propriétés du Carré Magique de Dürer

Le fascinant Carré Magique d’Albrecht Dürer
Sommaire1 La » Melencolia « 2 Les huit formes du Carré Magique de Dürer La » Melencolia « Le carré magique ci-dessous a été immortalisé par le peintre et graveur Albrecht Dürer (1471-1528), qui l’a représenté dans sa célèbre gravure, souvent reproduite, » Melencolia « , exécutée en 1514 : cette date figure dans les deux cases médianes de la dernière… Lire la suite »Le fascinant Carré Magique d’Albrecht Dürer

Les carrés magiques : Introduction
Le carré est l’un des quatre symboles fondamentaux avec le cercle, le centre et la croix. Tandis que le cercle symbolise le mouvement, la dynamique, au carré sont associés l’arrêt, la stabilité, la statique. Le carré est aussi le symbole de la matière terrestre, du corps et de la réalité, tandis que le cercle est… Lire la suite »Les carrés magiques : Introduction
Construction
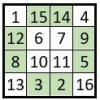
Construction des carrés magiques : La Méthode des nombres complémentaires sur les diagonales
Cette méthode inédite, permet de construire des carrés magiques en utilisant les nombres complémentaires sur les diagonales. Sommaire1 Carrés d’ordre n=42 Carrés d’ordre n=8 Carrés d’ordre n=4 On part du carré naturel d’ordre n = 4 ( Grille 1 ), dans lequel on remplace les nombres situés sur les diagonales centrales par leur complément à :… Lire la suite »Construction des carrés magiques : La Méthode des nombres complémentaires sur les diagonales
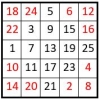
Construction des carrés magiques impairs : La méthode Conway
John Horton Conway ( 1937 – 2020 ) est un mathématicien britannique, bien connu en particulier, comme inventeur du Jeu de la Vie, entre autres. Dans la méthode de construction des carrés magiques normaux d’ordre impair, n=2 k + 1, mise au point par J. H. Conway, les nombres impairs et les nombres pairs sont… Lire la suite »Construction des carrés magiques impairs : La méthode Conway

Construction des carrés magiques : Un super carré magique d’ordre n = 9
Sommaire1 Introduction2 Propriétés3 Construction4 Dénombrement Introduction On considère la grille d’ordre n = 9, de 92 = 81 cases, comme constituée de 9 sous-carrés d’ordre n = 3, de 32 = 9 cases. On construit 9 sous-carrés d’ordre n = 3, avec les 9 séquences consécutives de 9 termes de la série ( 1 – 81… Lire la suite »Construction des carrés magiques : Un super carré magique d’ordre n = 9

Construction des carrés magiques impairs : La Méthode des permutations figurées
Cette méthode inédite est basée sur la propriété suivante du carré magique normal d’ordre impair : Dans le carré magique normal d’ordre impair, n = 2 k + 1, les termes de chaque sous-série naturelle, sont situés sur une permutation figurée. Prenons l’exemple de n=5. Les sous-séries naturelles se présentent ainsi dans le tableau ci-contre, sous la… Lire la suite »Construction des carrés magiques impairs : La Méthode des permutations figurées

Le talisman de Louis XIV
Sommaire1 Naissance de Louis XIV2 Une méthode de construction de ce talisman3 Une autre méthode de construction Naissance de Louis XIV A la naissance du fils de Louis XIII et d’Anne d’Autriche, le 5 septembre 1638, les astrologues de l’époque dressèrent l’horoscope du futur roi, dont faisait partie ce talisman, un carré magique d’ordre n… Lire la suite »Le talisman de Louis XIV
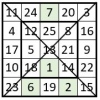
Construction des carrés magiques impairs : La Méthode des quatre Y
Cette méthode inédite s’applique aux carrés magiques d’ordre impair n = 2k + 1, avec k ≥ 2. La Méthode des quatre Y pour n = 5 Cette méthode a pour base l’une des formes du carré naturel de même taille, comme catalyseur. Nous prendrons comme catalyseur pour cet exemple le carré naturel « miroir » d’ordre… Lire la suite »Construction des carrés magiques impairs : La Méthode des quatre Y

Choix à priori de la constante linéaire des Carrés Magiques : Méthodes arabes
On se propose de rechercher comment on peut construire un carré magique, en nombres discontinus, lorsqu’on se donne a priori son ordre n et sa constante magique M’n. Sommaire1 Les nombres de base sont placés dans la première ligne1.1 Cas de n=31.2 Cas de n = 41.3 Cas de n = 51.4 Cas de n… Lire la suite »Choix à priori de la constante linéaire des Carrés Magiques : Méthodes arabes

Études et Jeux (2005-2015)
Sur cette page sont proposés des études, jeux, programmes… concernant les carrés magiques, écrits et réalisés par les lecteurs de ce blog. Si vous souhaitez également partager une de vos réalisations, contactez-nous !

Choix à priori de la constante linéaire des Carrés Magiques : Méthodes spéciales
Sommaire1 La Méthode d’Édouard Lucas. Cas de n = 3.2 La Méthode de Reichmann. Cas de n = 3.3 La Méthode de Bergholtz. Cas de n = 4.4 La méthode de Yu I. Ermakov. Cas de n = 4.5 Méthode de Labosne-Méziriac La Méthode d’Édouard Lucas. Cas de n = 3. La constante magique choisie… Lire la suite »Choix à priori de la constante linéaire des Carrés Magiques : Méthodes spéciales

Choix à priori de la constante linéaire des Carrés Magiques : Méthodes multiplicative et du quotient
Sommaire1 Méthode multiplicative2 Méthode du quotient Méthode multiplicative La relation classique de la division d’un nombre entier a par un nombre entier b est : a = b . q + rq étant le quotient et r le reste. Posons : a = M’n et b = MnEffectuons alors la division : M’n = Mn . q… Lire la suite »Choix à priori de la constante linéaire des Carrés Magiques : Méthodes multiplicative et du quotient

Construction des Carres Magiques : Les méthodes de Manuel Moschopoulos
Manuel Moschopoulos, un moine grec qui vivait vers 1392 en Crète, est l’auteur d’un très ancien traité des carrés magiques : on peut le dater du début du XVe siècle. Son manuscrit fut traduit en latin par Philippe de la Hire (1640-1718), mathématicien et astronome français, qui le communiqua à l’Académie des Sciences en 1691;… Lire la suite »Construction des Carres Magiques : Les méthodes de Manuel Moschopoulos

Construction des Carres Magiques : La Méthode du Cavalier d’Euler
Cette méthode est basée sur la » marche » du cavalier au jeu des échecs. Elle a été mise au point par le mathématicien bâlois Leonhardt Euler (1707-1783), notamment dans une communication intitulée « De quadratis magicis » (StPetersbourg, 1776) Rappelons qu’à partir d’une case donnée de l’échiquier, le cavalier peut de déplacer de 8 façons différentes,… Lire la suite »Construction des Carres Magiques : La Méthode du Cavalier d’Euler

Construction des Carres Magiques : La Méthode de Ralph Strachey
Ralph Strachey (1868-1923) fut ingénieur civil en Inde. La Méthode de Ralph Strachey s’applique : aux carré d’ordre n = 2(2k+1), ou » impairement pairs « , c’est-à-dire à n = 6, 10, 14, 18, 22… aux carrés d’ordre n = 4k ou » pairement pairs « , c’est-à-dire à n = 4, 8, 12, 16… Carrés d’ordre n = 2(2k+1)… Lire la suite »Construction des Carres Magiques : La Méthode de Ralph Strachey

Construction des carrés magiques : La Méthode de El‑Bouni
El-Bouni, qui décrit cette méthode de construction des carrés magiques à enceinte(s) d’ordre impair, est originaire de Bône (Algérie) ; il est mort en 1225. On peut situer l’ouvrage dans lequel il traite des carrés magiques, au début du XIIIème siècle. D’après le traducteur/commentateur de El-Bouni, l’origine persane de cette méthode transparaît dans le texte… Lire la suite »Construction des carrés magiques : La Méthode de El‑Bouni

Construction des Carres Magiques : Méthode de Benjamin Franklin
Benjamin Franklin ( 1706-1790), homme politique et homme de sciences américain, est l’auteur d’une méthode de construction des carrés magiques d’ordre n = 8 originale. Cette méthode nécessite deux carrés auxiliaires indicés. I – Le carré auxiliaire I est le carré naturel N. II – Dans la grille II, on place les lettres » A,B,C,D….H » dans… Lire la suite »Construction des Carres Magiques : Méthode de Benjamin Franklin

Construction des Carres Magiques : La Méthode de De La Hire
Philippe de La Hire (1640-1718) fut poussé vers la peinture par son père Laurent de La Hire, qu’il étudie à Rome. A partir de 1664,de retour à Paris, Philippe de La Hire se tourna vers les sciences et montra des intérêts très diversifiés : cartographe du royaume, il s’intéressa à la géométrie, à l’hydraulique, à… Lire la suite »Construction des Carres Magiques : La Méthode de De La Hire

Construction des Carres Magiques : La Méthode de François Spinula
François Spinula (Francisci Spinulae), un père jésuite, décrit dans son ouvrage : De intercalandi ratione corrigenda & de tabellis quadratorum numerorum à Pythagoreis dispositorum (1562), une méthode de construction des carrés magiques normaux d’ordre pair, de la forme n = 4k. On peut présenter cette méthode de la manière suivante. Exemple pour n = 4.… Lire la suite »Construction des Carres Magiques : La Méthode de François Spinula

Construction des Carres Magiques : La Méthode de Bachet de Méziriac
Claude Gaspard Bachet de Méziriac (1581-1638), dans ses » Problèmes plaisants et délectables qui se font par les nombres » (1612), restés célèbres, donne une méthode simple pour la construction des carrés magiques d’ordre impair. Cette méthode est très connue. Soit l’exemple d’un carré magique d’ordre n = 5. On écrit les n2 = 25… Lire la suite »Construction des Carres Magiques : La Méthode de Bachet de Méziriac
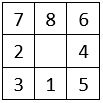
Les carrés multiples
Je nomme « Carrés multiples », une grille numérique carrée d’ordre « n », remplie avec les n2 premiers entiers, dont tous les alignements de n chiffres, quel que soit le sens de lecture, forment des nombres multiples d’un nombre donné. Sommaire1 Les carrés multiples de 3 : Le Lo Shu2 Les carrés multiples de 93 Des carrés multiples à trou… Lire la suite »Les carrés multiples
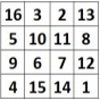
La construction du Carré Magique de Dürer
Il existe plusieurs méthodes de construction du carré magique de Dürer. En voici quelques-unes. Sommaire1 La Méthode des permutations sur les diagonales2 La Méthode des permutations3 La Méthode des pointages4 La Méthode des « inversions » ou des « symétries » La Méthode des permutations sur les diagonales On part du carré fondamental naturel (1) On permute les nombres… Lire la suite »La construction du Carré Magique de Dürer
Art, Documents et Biographies

Nicolas de Cues et la quadrature du cercle
Nicolas de Cues (1401 – 1464), de son vrai patronyme Nikolaus Krebs, connu aussi sous le nom de Nicolas de Cuse, est un théologien, philosophe, humaniste, mathématicien et prélat allemand, né à Cues, dans le territoire du Westrich (Palatinat).Docteur en Droit, il est nommé cardinal en 1448, puis évêque de Brixen en 1450. Nicolas de… Lire la suite »Nicolas de Cues et la quadrature du cercle

L’art de Pascale Renaud
Pascale Renaud est née en 1969 dans les Ardennes françaises ; elle vit et travaille près de Grenoble (Alpes). Peintre autodidacte, elle pratique l’acrylique et participe à différentes expositions et salons depuis début 2006. Ses créations sont principalement abstraites et basées sur le carré. Elles peuvent avoir un sens, ou pas, selon la lecture que chacun… Lire la suite »L’art de Pascale Renaud

Les carrés magiques de Yolande Bastoni
Yolande Bastoni est née en 1961 à Martigues, a partir de 1980 , elle fréquente l’Ecole des Arts Décoratifs de Nice et dès 1981 , elle entre à l’Ecole des Beaux-Arts d’Aix-en-Provence. Après diverses expériences à succès dans les arts graphiques et arts décoratifs, elle s’engage résolument vers l’abstraction.Yolande Bastoni s’inscrit dans le mouvement de l’art… Lire la suite »Les carrés magiques de Yolande Bastoni

Art Abstrait et Carrés
Le carré, forme géométrique parfaite à quatre côtés égaux, a inspiré de nombreux architectes et artistes peintres. Le carré, par sa modernité, est à l’origine de nombreuses œuvres d’arts et a toujours constitué un défi pour beaucoup d’artistes.Cette page montre une sélection de quelques œuvres utilisant le carre comme base de composition.

L’art de Jean-Michel Raczinski
Jean-Michel Raczinski né en 1957 vit et travaille à Paris. Il pratique la peinture depuis l’enfance et a suivi les cours de l’École du Louvre. Ingénieur passionné de musique, il a travaillé près de 18 ans auprès du compositeur Iannis Xenakis sur des outils informatiques d’aide à la composition musicale. La géométrie plus ou moins visible… Lire la suite »L’art de Jean-Michel Raczinski

Cabinet de curiosités carrées
Quelques objets liés aux carrés (souvent magiques), inclassables et surprenants…

Études et Jeux (2005-2015)
Sur cette page sont proposés des études, jeux, programmes… concernant les carrés magiques, écrits et réalisés par les lecteurs de ce blog. Si vous souhaitez également partager une de vos réalisations, contactez-nous !

Michael Stifel
On attribue souvent l’invention des carrés magiques à enceintes, ou à bordures, à Bernard Frénicle de Bessy (1693), ou même à Blaise Pascal (1654).En réalité ce type de carré magique, qui a suscité de nombreuses études et méthodes de construction, a été présenté pour la première fois en Occident par Michael Stifel dans son ouvrage… Lire la suite »Michael Stifel

Les peintures de Jean François Motte
Jean François Motte , né en 1955. Pratique assidûment la photographie tant en prise de vue qu’en laboratoire depuis l’adolescence, activité qu’il poursuivra au sein du Club Photographique de LILLE durant ses études dans le champ de la santé mentale. Participe dès 1984 à l’animation d’un atelier d’art-thérapie. Ce qui l’amène dès lors au dessin et… Lire la suite »Les peintures de Jean François Motte

Les carrés magiques en Architecture et Urbanisme.
Sommaire1 Fresques, mosaïques et sculptures2 Le carré Sator Fresques, mosaïques et sculptures Des carrés magiques ont été fréquemment représentés au cours des ages, sur différent supports.En voici quelques exemples: Le carré Sator Le carré Sator, palindrome véhiculé par le Christianisme depuis au moins 16 siècles, a fait couler beaucoup d’encre. En effet, on suppose qu’il… Lire la suite »Les carrés magiques en Architecture et Urbanisme.

Claude Gaspard Bachet de Méziriac
Claude Gaspard Bachet de Méziriac est né le 9 octobre 1581 à Bourg-en-Bresse, dans une famille de notables, magistrats, juristes, tous lettrés. Il fait de solides études chez les Jésuites, à Turin puis à Padoue. Il enseigne lui-même à Milan, à Côme, maîtrisant parfaitement le latin, le grec, l’italien. Revenu en France, il partage son… Lire la suite »Claude Gaspard Bachet de Méziriac

Polyominos : Pentaminos, Katamino et Tetris
Le terme polyomino a été utilisé par Solomon Golomb en 1953 pendant une conférence du Harvard Mathematics Club et plus tard dans un article du American Mathematical Monthly. Il définit un polyomino comme des carrés joints a un autre carré au moins par un coté. L’ordre d’un polyomino est le nombre de carrés utilisés pour… Lire la suite »Polyominos : Pentaminos, Katamino et Tetris

Jeux des carrés magiques
Ces jeux sont des applications directes des propriétés des Carrés Magiques.Les joueurs doivent former un carré de nombres dont la somme des lignes horizontales, verticales et les diagonales doit être égale à une constante magique.

Documents et Médias liés aux carrés magiques
De nombreux livres, films et autres supports utilisent les carrés magiques comme élément de scenario ou de représentation. Quelques exemples sont listés ici.Sont exclus les ouvrages de référence sur les méthodes de construction, d’analyse des carrés magiques.

Le néoplasticisme de Piet Mondrian
Piet Mondrian (1872-1944), peintre néerlandais, pionnier de l’art abstrait, auquel il donna une de ses formulations les plus rigoureuses, à la fois comme plasticien et comme théoricien.Pieter Cornelis Mondriaan, qui changea l’orthographe de son nom en Mondrian à Paris en 1912, est né à Amersfoort, aux Pays-Bas, le 7mars 1872. La découverte du cubisme à Paris,… Lire la suite »Le néoplasticisme de Piet Mondrian

Le carré magique de Gaudi
Sur l’une des façades de la « Sagrada Familia », la cathédrale de Barcelone, se trouve sculpté dans la pierre, un carré numérique, dont la constante « magique » est M’4 = 33, soit l’âge présumé de Jésus Christ lorsqu’il a été crucifié. Notons également que la somme des quatre cases centrales est également égale à 33. C’est Antoni… Lire la suite »Le carré magique de Gaudi

Collages et dessins de René Descombes
René Descombes est à l’origine de la plupart des articles de ce blog.Il s’est également amusé à réaliser différents collages et dessins en rapport avec les carrés magiques Les côtés des cases forment une progression arithmétique décroissante, puis croissante, de raison r = 0,4 mm, dans chaque ligne et chaque colonne dans cette grille de… Lire la suite »Collages et dessins de René Descombes

Les échecs de Gérard Louis Gautier
Gérard Louis Gautier (1948) a suivi une formation universitaire en lettres modernes et linguistique générale. Après quelques années d’enseignement comme professeur de français, il opte pour le dessin de presse en 1976.Passionné de cinéma, il débute comme illustrateur dans la revue Ecran tout en plaçant divers dessins d’humour dans le magazine pour jeunes Formule I. Suite… Lire la suite »Les échecs de Gérard Louis Gautier

Les carrés de Hannes Bürgel
Hannes Bürgel (1927-2023), ancien professeur d’histoire de l’art de l’Université de Dresde, est l’auteur de nombreux livres sur l’art et l’architecture. Il s’est également intéressé aux carrés magiques et leur construction, et a produit de nombreuses illustrations dérivées des carrés magiques.